[GECCO 2024] GPU-accelerated Evolutionary Multiobjective Optimization Using Tensorized RVEA

Zhenyu Liang, Tao Jiang, Kebin Sun, Ran Cheng

Abstract

Evolutionary multiobjective optimization has witnessed remarkable progress during the past decades. However, existing algorithms often encounter computational challenges in large-scale scenarios, primarily attributed to the absence of hardware acceleration. In response, we introduce a Tensorized Reference Vector Guided Evolutionary Algorithm (TensorRVEA) for harnessing the advancements of GPU acceleration. In TensorRVEA, the key data structures and operators are fully transformed into tensor forms for leveraging GPU-based parallel computing. In numerical benchmark tests involving large-scale populations and problem dimensions, TensorRVEA consistently demonstrates high computational performance, achieving up to over 1000× speedups. Then, we applied TensorRVEA to the domain of multiobjective neuroevolution for addressing complex challenges in robotic control tasks. Furthermore, we assessed TensorRVEA’s extensibility by altering several tensorized reproduction operators. Experimental results demonstrate promising scalability and robustness of TensorRVEA. Source codes are available at https://github.com/EMI-Group/tensorrvea.

Method

The implementation of the TensorRVEA algorithm is the result of deeply integrating tensorization techniques and GPU acceleration technology, which greatly enhances the efficiency of solving multiobjective optimization problems. Tensorization, a technique for converting data structures and operations into tensor forms, is particularly well-suited for efficient parallel processing on GPUs. This provides a novel solution for large-scale optimization problems.

In the TensorRVEA algorithm, the application of tensorization is first reflected in the conversion of key data structures. Populations, objective vectors, and reference vectors are all represented in tensor form. This not only makes the data representation more compact but also allows the algorithm to process the entire population at once, rather than individually, thereby significantly improving computational efficiency.

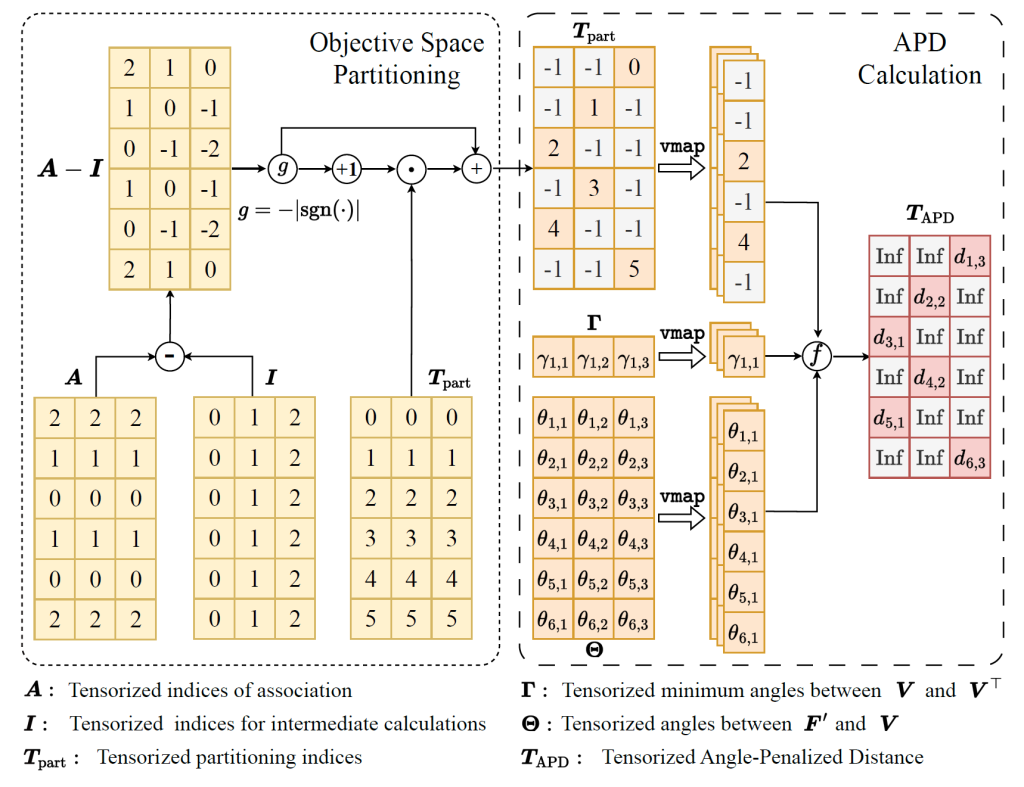
The TensorRVEA algorithm implements fitness evaluation, crossover, mutation, and selection operations through full tensor operations, significantly enhancing the efficiency of multiobjective optimization. The core of the algorithm lies in the tensorized selection mechanism. This mechanism involves translation and normalization, objective space partitioning, calculation of the Angle Penalized Distance (APD), and selection of elite individuals. This effectively drives the population towards the Pareto optimal front. In this process, the population is intelligently divided into multiple sub-populations based on the closeness of their angles to various reference vectors. Each sub-population independently selects individuals based on the APD, which combines the angle and distance between individuals and reference vectors to balance the convergence and diversity of the population. The following example illustrates the population partitioning and APD calculation in a situation where the population size is 6 and the number of reference vectors is 3. This vividly reflects how the algorithm transforms the original multiple loops into efficient full tensor operations.

Results

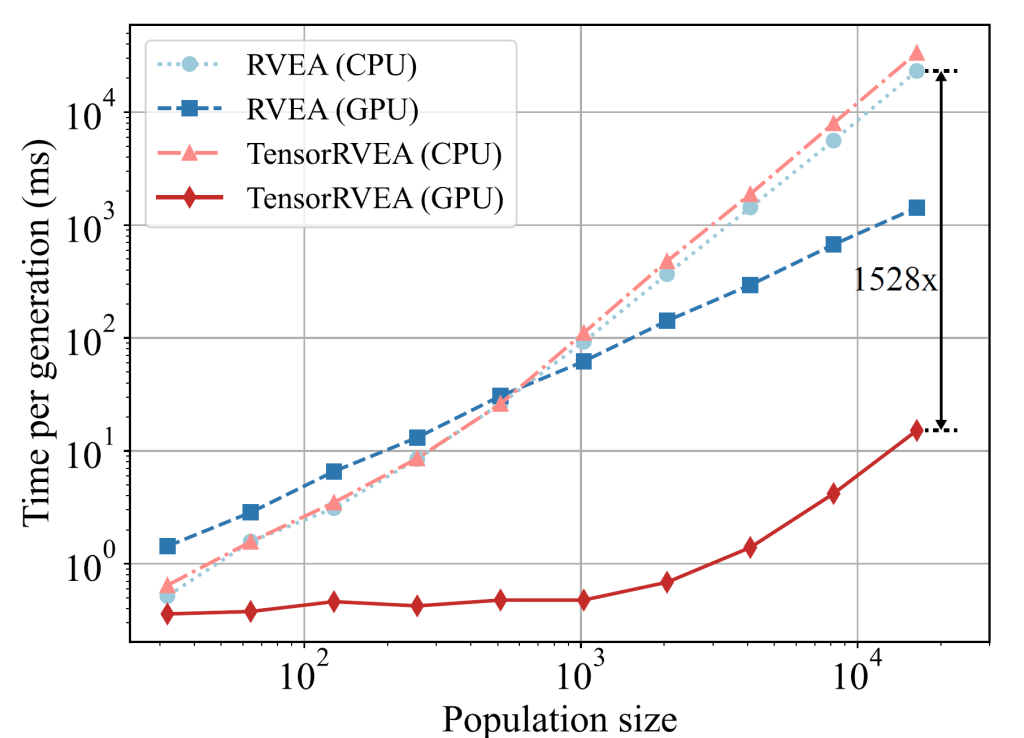
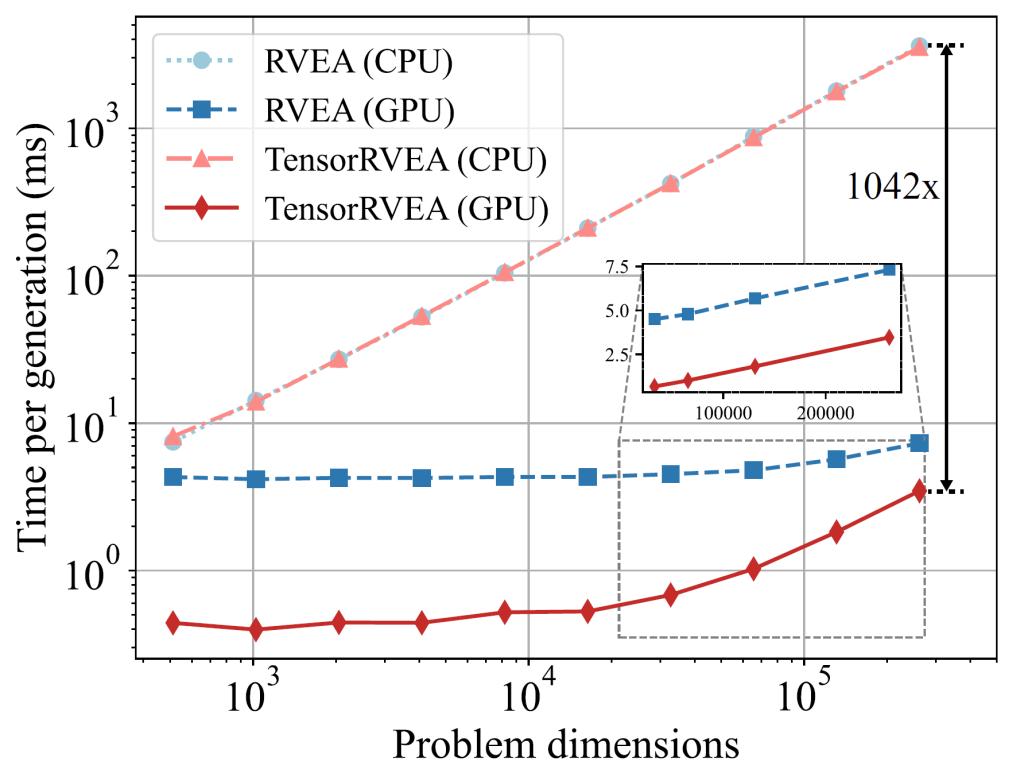
To verify the performance of TensorRVEA, the research team conducted a series of experiments, including acceleration performance, numerical benchmark tests, multiobjective neuroevolution, and algorithm scalability. In the acceleration performance experiment, TensorRVEA showed speed improvements of up to 1528 times and 1042 times compared to RVEA (CPU) when dealing with large-scale populations and high-dimensional problems.

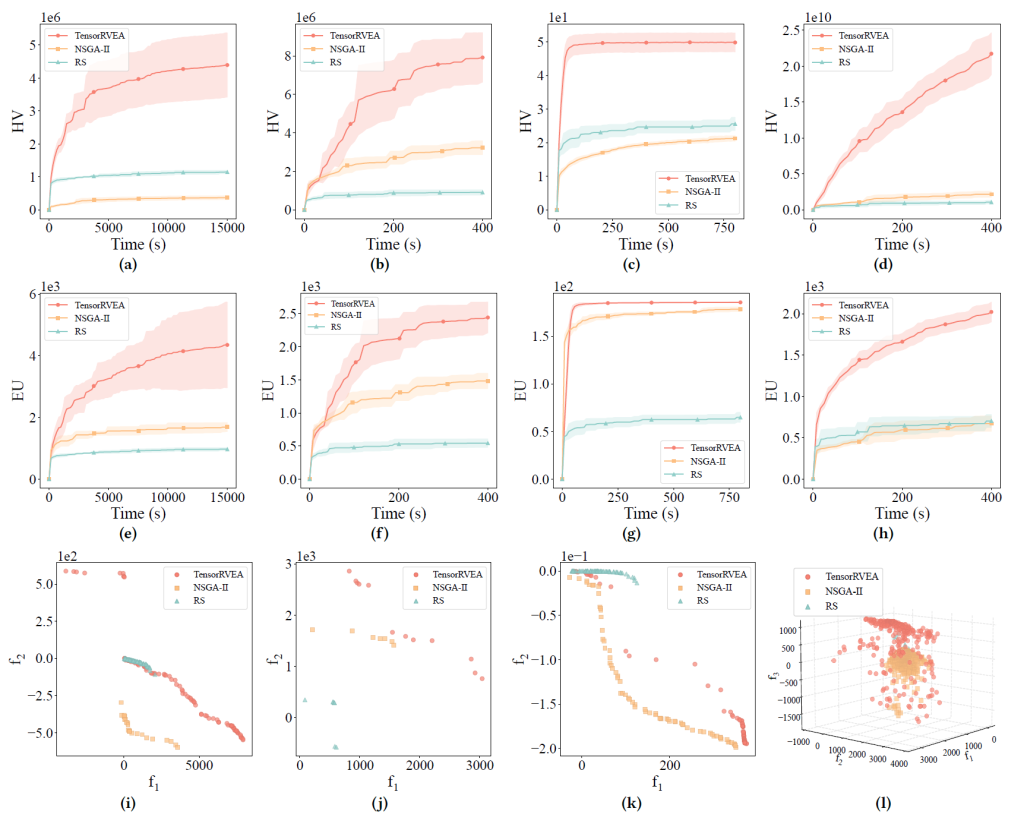
In the multiobjective neuroevolution experiment, the research team cleverly extended Brax to transform its single-objective problems into multiobjective optimization problems. They applied three algorithms: TensorRVEA, NSGA-II, and random search, to the field of neuroevolution to solve multiobjective robotic control problems. In these experiments, the algorithms were used to optimize the parameters of Multi-Layer Perceptron (MLP) networks, which act as policy models to drive robots to complete specific control tasks. The results showed that TensorRVEA exhibited significant high-performance advantages in handling these computationally intensive and complex robotic control tasks, further verifying its potential application in real engineering problems.

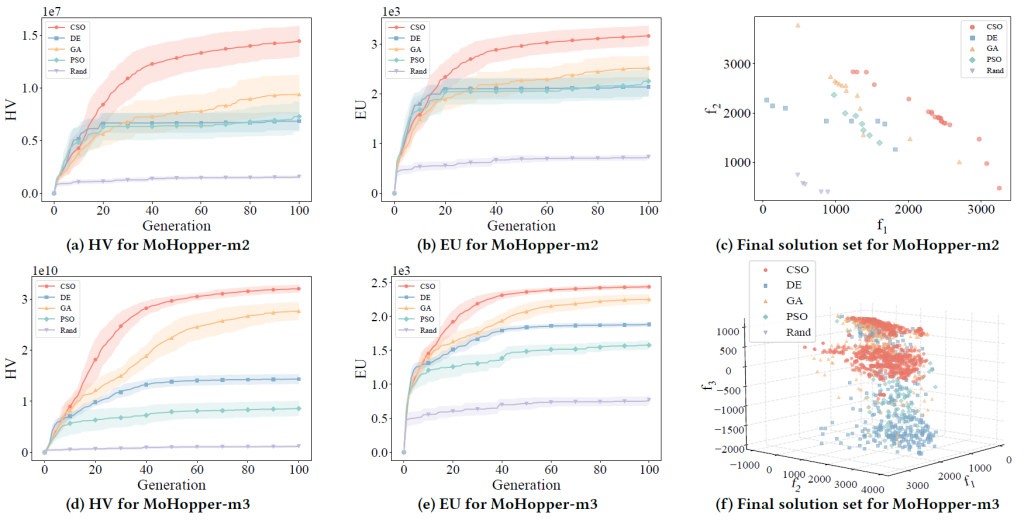
Finally, in the scalability experiment, by integrating different generative operators like GA, PSO, DE, CSO, and random generation, TensorRVEA demonstrated good adaptability and flexibility.

Conclusion

This study successfully demonstrates the application of tensorization and GPU acceleration in Evolutionary Multiobjective Optimization (EMO) through the TensorRVEA algorithm, effectively enhancing the capability to handle large-scale and multiobjective problems. TensorRVEA exhibited exceptional computational speed and performance across a range of optimization challenges, including traditional numerical benchmarks and complex robotic control tasks. The results confirm the advantages of its design, especially in integrating various generative operators, showing good scalability. Future research will continue to explore tensorization in EMO algorithms and may develop frameworks and operators specifically designed for GPU acceleration.

@inproceedings{tensorrvea, 
  title = {{GPU}-accelerated {Evolutionary} {Multiobjective} {Optimization} {Using} {Tensorized} {RVEA}}, 
  author = {Liang, Zhenyu and Jiang, Tao and Sun, Kebin and Cheng, Ran},  
  booktitle = {Proceedings of the Genetic and Evolutionary Computation Conference (GECCO)}, 
  year = {2024}
}