One paper accepted by IEEE TCYB

One paper accepted by IEEE TCYB

Recently, the EMI research group has made progress in the research field of large-scale dynamic optimization. The work is entitled “Evolutionary Large-Scale Dynamic Optimization Using Bilevel Variable Grouping” and published in the famous academic journal “IEEE Transactions on Cybernetics” (IEEE TCYB, impact factor: 11.448).

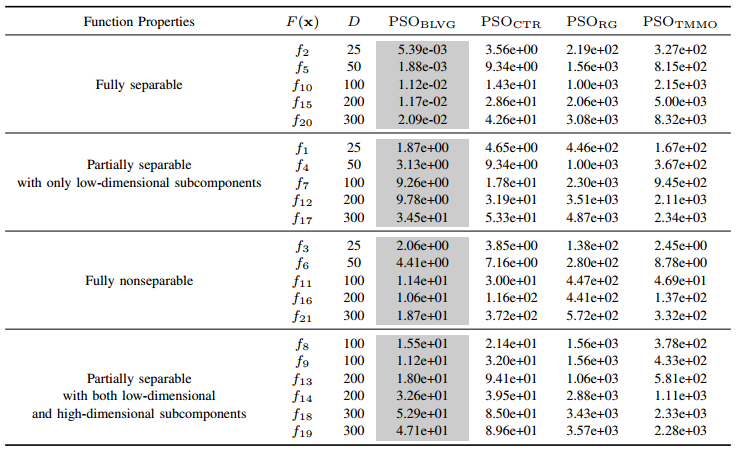
Currently, most research on large-scale optimization focuses on problems in static environments, while few studies have focused on dynamic optimization. Many large-scale static optimization problems can be regarded as dynamic due to intrinsic uncertainties and environmental changes. For example, the weight optimization problems in deep learning are large-scale by nature and the arrival of new training data makes online learning a dynamic problem; the search space of large-scale crossing waypoints located in air route networks changes by delayed airplanes, breakdowns, and extreme weather conditions. The difficulty of the large-scale dynamic optimization problems is how to find the optimal solutions with a large number of variables and then track them after environmental changes with limited computational resources. This work proposes a bilevel variable grouping framework (BLVG) and tailors multi-population strategies for various variable groups, which achieves an effective performance on large-scale dynamic optimization problems of up to 300 dimensions.

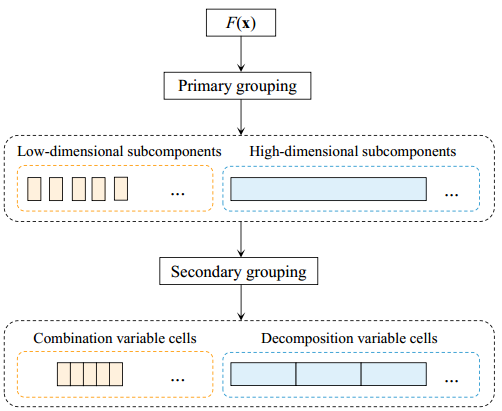
Researchers analyze the pros and cons of the state-of-the-art algorithms and point out that when the numbers/sizes of the variable subcomponents are large, the performance of the algorithms will be substantially degraded, and variable grouping is not well studied in large-scale dynamic optimization when cooperating with multi-population strategies. Hence, they propose a bi-level variable grouping-based framework. First, the primary grouping applies a state-of-the-art variable grouping method based on variable interaction analysis to group the variables into subcomponents. Second, the secondary grouping further groups the subcomponents into variable cells, i.e., combination variable cells and decomposition variable cells, such that a moderate number of dimensions for variable cells can be obtained to make full use of an optimizer. Then a multi-population strategy is designed to process the two types of variable cells efficiently in a cooperative coevolutionary way.

The first author of this article is Hui Bai, a Ph.D. student of the EMI research group, and Ran Cheng, the Associate Professor of the EMI research group, is the corresponding author of the paper. The collaborators also include Danial Yazdani, Research Assistant Professor of SUSTech, Kay Chen Tan (IEEE Fellow), Professor of Hong Kong Polytechnic University, and Yaochu Jin (IEEE Fellow), Professor of the University of Surrey, UK.

 

Fig. 1. An illustration of the proposed bilevel variable grouping method. F(x) is an original problem. In primary grouping, the decision vector in the original problem is grouped into low-dimensional subcomponents (e.g., 1-dimensional subcomponents) and high-dimensional subcomponents (e.g., 30-dimensional subcomponents) by DG2. Then in the secondary grouping, every five low-dimensional subcomponents are regrouped into a combination variable cell, and each high-dimensional subcomponent is further decomposed into three decomposition variable cells in the figure.

 

Table 1. Comparison results of BLVG and other three frameworks using PSO optimizer on four types of large-scale DOPs. The highlighted entries are significantly better using pairwise Wilcoxon signed-rank tests with Holm-Bonferroni p-value correction with α = 0.05. The results demonstrate that PSOBLVG performs significantly better than the others.

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注